Hiểu công thức bước sóng giúp ứng dụng gì trong thực tế?

Khi bạn đang xem xét ánh sáng khả kiến, sóng vô tuyến hay bất kỳ loại sóng nào khác, việc biết cách tính bước sóng là rất quan trọng để hiểu được hành vi của sóng và các ứng dụng của chúng trong nhiều lĩnh vực khoa học khác nhau.

Bước sóng là gì?

Bước sóng (λ) đề cập đến khoảng cách giữa các điểm liên tiếp của sóng hình sin cùng pha với nhau. Nói cách khác, đó là độ dài một chu kỳ hoàn chỉnh của sóng, được đo từ đỉnh này (điểm cao nhất) đến đỉnh tiếp theo hoặc từ đáy này (điểm thấp nhất) đến đáy tiếp theo.

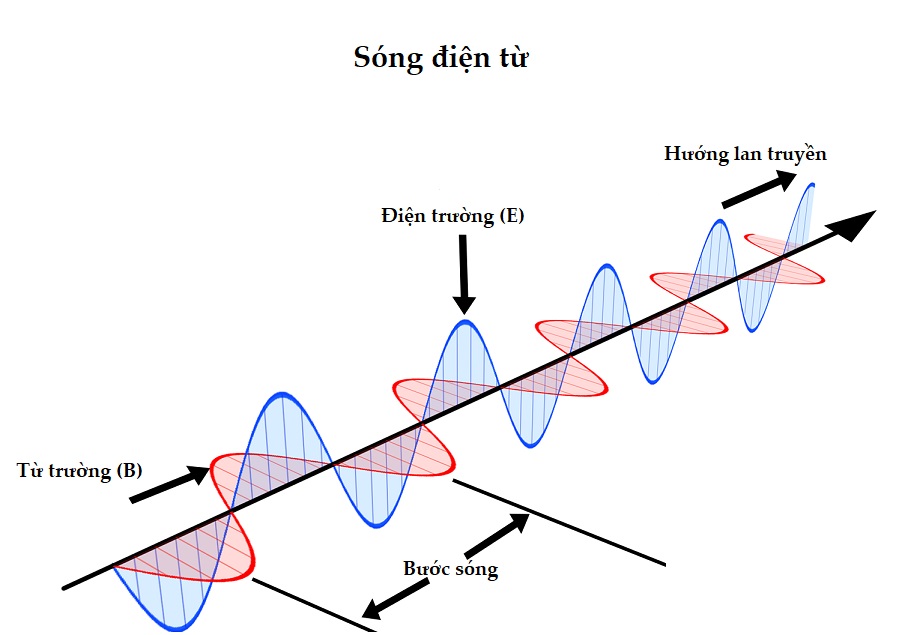
Cho dù đó là ánh sáng khả kiến, sóng vô tuyến, vi sóng hay tia X, mỗi loại sóng điện từ đều có bước sóng riêng. Ví dụ, ánh sáng khả kiến gồm các màu khác nhau, mỗi màu tương ứng với một bước sóng cụ thể trong quang phổ.

Công thức tính bước sóng

Công thức tính bước sóng là: λ = v / f, trong đó λ là bước sóng, v là vận tốc sóng, f là tần số của sóng.

Biết được vận tốc và tần số sóng, cho phép xác định chính xác bước sóng tại một điểm nhất định. Công thức này làm nổi bật mối quan hệ tỉ lệ nghịch giữa bước sóng (λ) và tần số (f). Khi cái này tăng thì cái kia giảm và ngược lại.

Bước sóng thường được đo bằng mét (m), vận tốc sóng tính bằng mét trên giây (m/s), tần số tính bằng hertz (Hz). Công thức bước sóng là công cụ thiết thực cho các nhà khoa học và kỹ sư, sử dụng rộng rãi trong việc tìm hiểu sóng điện từ, gồm toàn bộ quang phổ điện từ.

3 ứng dụng của công thức bước sóng

Công thức bước sóng có nhiều ứng dụng trong thực tế, trong đó có một số ứng dụng cụ thể sau:

1. Quang phổ mặt trời: Ánh sáng Mặt trời chiếu đến Trái đất trải dài trên một quang phổ các bước sóng, từ tia cực tím đến tia hồng ngoại. Việc hiểu công thức bước sóng rất quan trọng trong nghiên cứu nhiều lĩnh vực khoa học, trong đó có cả thiên văn và khí hậu.

2. Tín hiệu truyền thông: Trong lĩnh vực viễn thông, sóng vô tuyến mang các tín hiệu có bước sóng cụ thể. Các kỹ sư và kỹ thuật viên sử dụng công thức bước sóng để thiết kế ăng-ten và tối ưu hóa việc truyền tín hiệu.

3. Chụp ảnh y tế: Trong lĩnh vực y tế, việc hiểu được bước sóng của tia X rất quan trọng đối với các kỹ thuật như chụp X-quang và chụp cắt lớp vi tính (CT).